Description
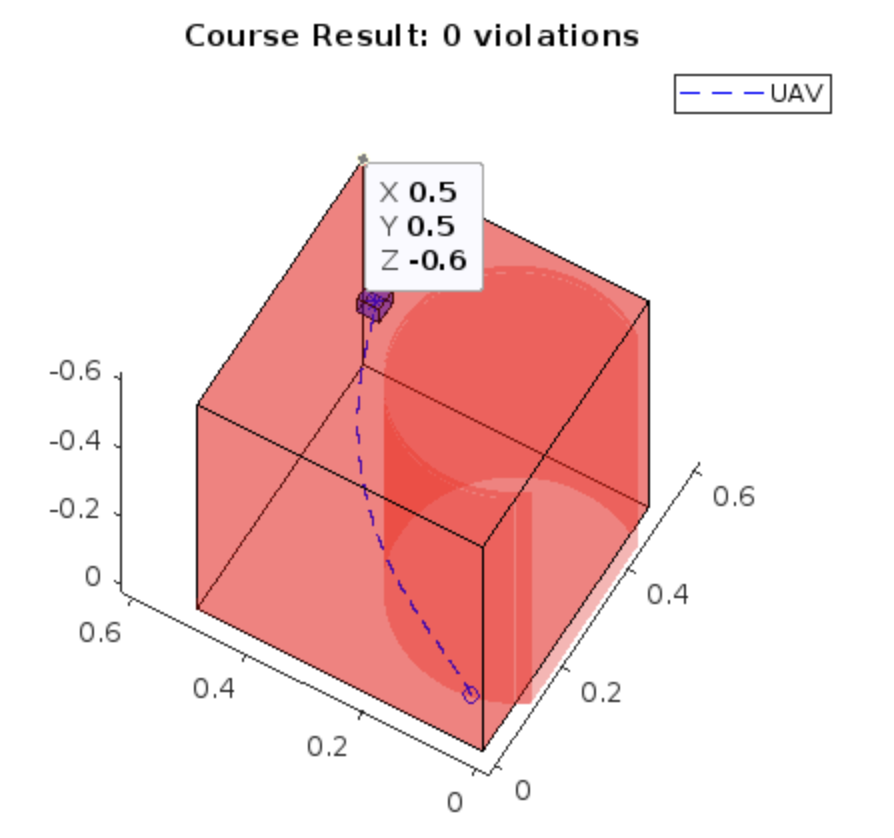
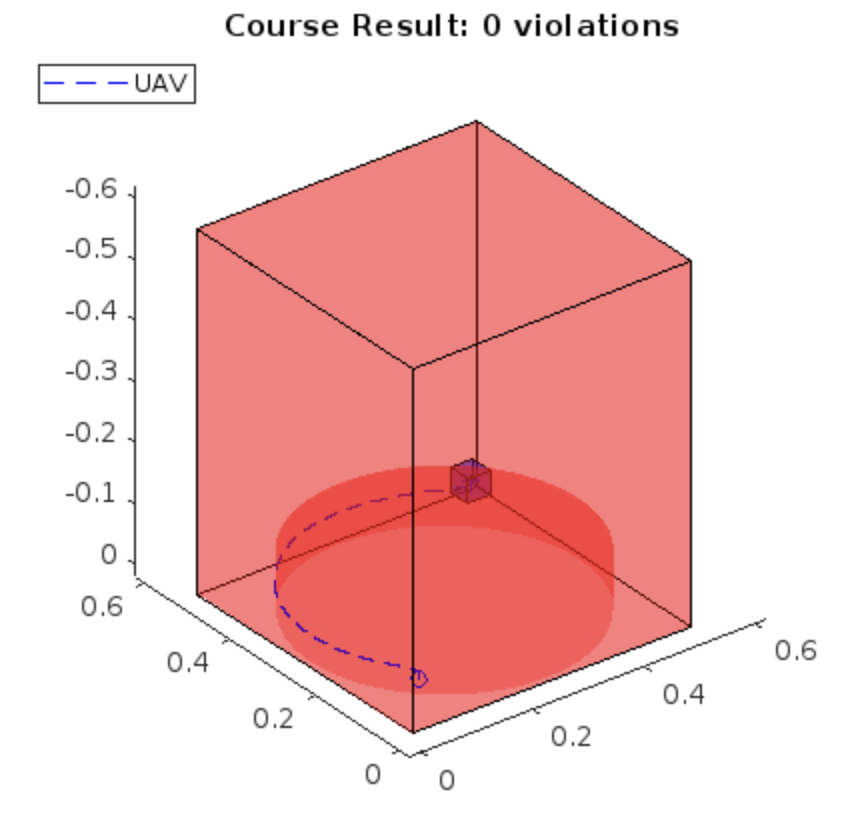
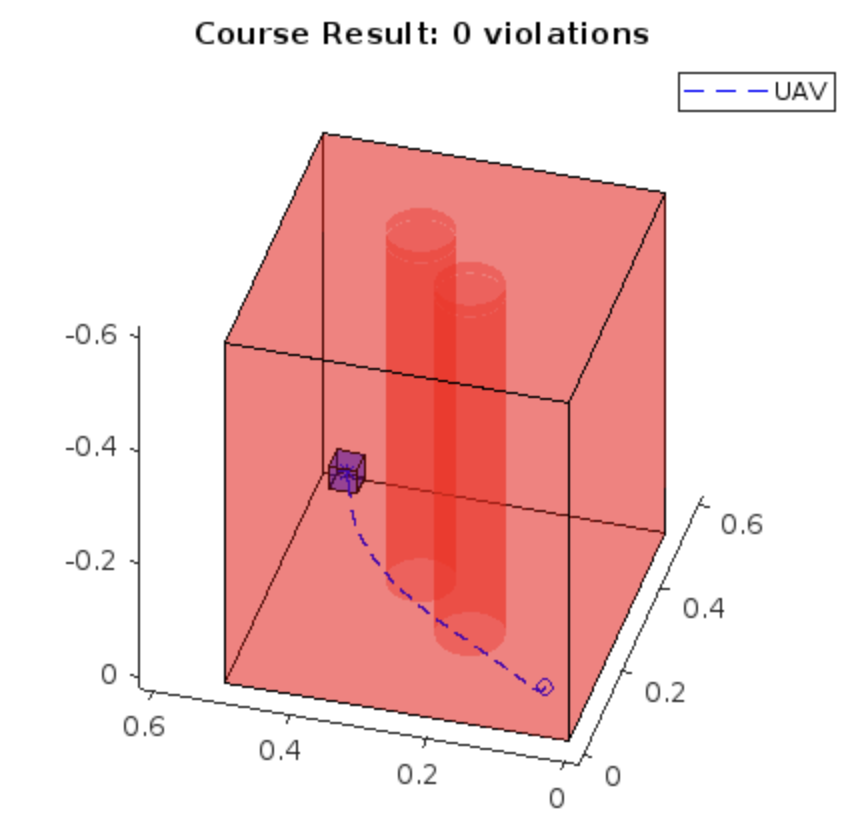
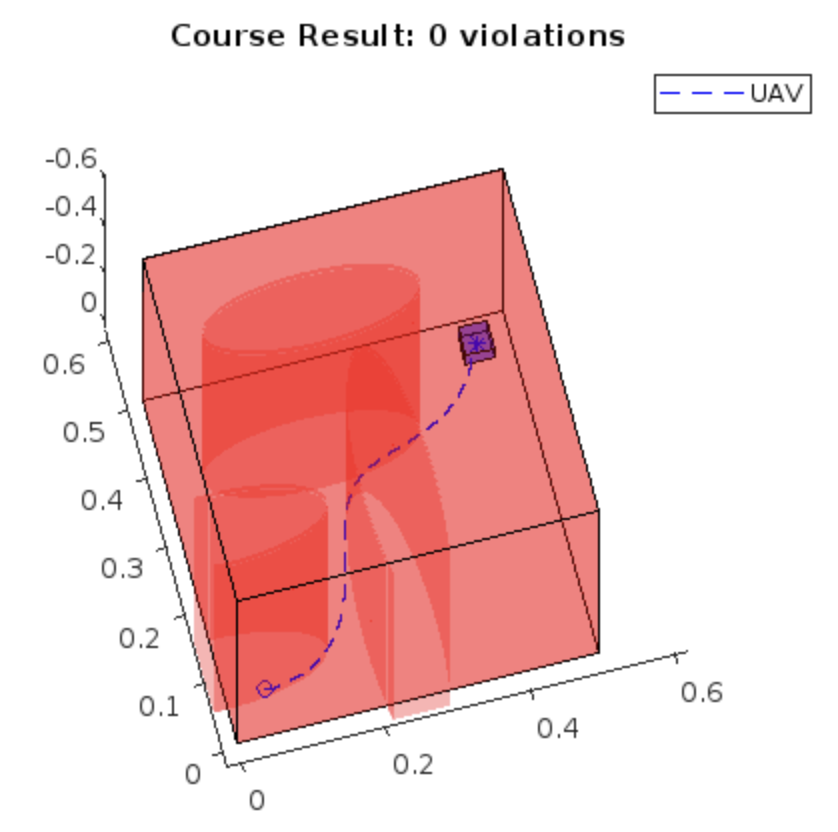
Coursework for the Predictive Control Module run by Professor Eric Kerrigan. The objective was to design a Model Predictive Controller for a simulated Quadrotor capable of flying between an initial and target point whilst avoiding elliptical obstacles; all within a certain amount of time.
Details
| Skills: | Model Predictive Control Linear Algebra Matlab |
| Scope: | University |
| Date: | March 2024 |
Features
- Nonlinear Dynamics : System dynamics were included in the optimal control problem by making use of numerical integration methods. Initial tests were conducted using Explicit Euler which worked but had large initial errors of ~0.614 (error after the first controller iteration) resulting in early inequality violations and slower guess convergence. An improved performance was demonstrated by RK4 with an error of ~0.121. Despite it's performance, accuracy issues occurred when testing with ellipse constraints, resulting in undesirable constraint violations. The method settled upon was the implicit Trapezoidal rule which although less accurate (initial error of ~0.278) resulted in improved constraint adherence ( as implicit methods work better with stiff functions ). To account for the full nonlinear dynamics of the quadrotor these equilibrium constraints were computed during runtime with the system being discretized for each optimisation step. Overall this resulted in accurate state predictions, provided additional flexibility in parameter tuning and reduced the likelihood of model failure due to the simplifications imposed by linearisation. This all came at the cost of an increased computational load as large matrices had to be rapidly constructed, resulting in even simple courses taking significant amounts of time to run.
- Dynamic Inequalities : Due to the obstacles, nonlinear constraints had to be implemented for collision avoidance which was done through a number of auxiliary variables. By imposing linear constraints on the auxiliary variables and adding them to the state to be optimised it was possible to impose an OR inequality, valid when the quadrotor was above OR outside of the ellipses, allowing for full obstacle avoidance.
- Temporal Costs : A number of temporal costs where also necessary to complete the tasks as the quadrotor had to complete courses within a certain amount of time (bounds cost) and with a total thrust above equilibrium below a certain amount (thrust cost).
- Robustness : A number of additions were made to make the controller robust to uncertainties and unseen shapes. An important variable is the equilibrium thrust, a value which changes when perturbations are applied to the model. This causes major issues as this value is used for the thrust cost, resulting in possible course failure due to incorrect punishment. To estimate this parameter a 'drop test' is conducted during the first time step, where the nominal equilibrium thrust is provided and the change in the z velocity is measured on the next. By calculating the actual acceleration and comparing it to the nominal, it is possible to calculate the equilibrium thrust needed with the perturbations in place.